En este artículo se describen los pasos que llevaron al diseño y construcción de un reloj de sol doble horizontal utilizando los trabajos desarrollados por Samuel Foster sobre relojes de sol elípticos reticulares.

Introducción

Se denominan autorientables aquellos relojes de sol que por su diseño permiten la alineación con la meridiana. Siempre me ha llamado la atención esta característica que facilita su uso y añade la posibilidad de utilizarlos para encontrar el Norte.

Para conseguir ser autorientables, algunos diseños incorporan dos relojes de sol horizontales, cada uno de ellos utilizando un parámetro distinto del movimiento del Sol, por ejemplo, acimut y ángulo horario.

Dos ejemplos de este tipo de relojes de sol doble horizontales y auto orientables son:

el doble horizontal de proyección estereográfica inventado por William Oughtred.
el doble horizontal Analemático inventado por Jean-Louis de Vaulezard.

En este último, la necesidad de desplazar el índice o gnomon del Analemático cada día y mantenerlo fijo mientras se movía el plano del cuadrante para encontrar el norte, me parecía engorroso y sujeto a los errores de posicionar correctamente el índice.

A principios de este año, para el desarrollo de una nueva app, estuve investigando el cálculo de distintos tipos de relojes de sol de acimut que tuviesen un gnomon fijo. El primero fue el que utiliza la proyección estereográfica y a continuación empecé a investigar los analemáticos.

Buscando información encontré el articulo “Analemmatic Sundial With Fixed Gnomon” de J.A. Sassenburg [1] y profundizando llegue al artículo “Elliptical Sundials: General & Craticular” de Fred Sawyer [2] que ofrece un desarrollo completo de los estudios y escritos de Samuel Foster sobre los relojes de sol elípticos y establece las fórmulas para poder calcular cualquier tipo de reloj de sol Analemático con índice fijo.

Ya tenía las herramientas necesarias para diseñar un reloj de sol analemático en el que no hiciese falta mover el índice.

Diseño

Después de estudiar cuidadosamente el documento de Fred, creé un libro de Excel con las fórmulas generales de forma que pudiese experimentar modificando los diversos parámetros y ver el resultado. En este paso, el programa Alemma de Helmut Sonderegger [3] me fue de mucha ayuda para comprobar la coherencia de los resultados obtenidos.

Las ecuaciones utilizadas son las que se encuentran en las páginas 29 y 30 del artículo de Fred [4].

Dándole al índice o estilo una inclinación de (90+Φ)/2 respecto al horizonte, o siguiendo la nomenclatura del programa Alemma (90-Φ)/2, las elipses de un analemático clásico se convierten en circunferencias. Si en vez de mover el índice lo mantenemos fijo y trazamos una circunferencia para cada valor de la declinación del Sol y hacemos que todas las líneas de horas converjan en el punto de 24 horas de la circunferencia para los equinoccios, se obtiene el siguiente diseño.

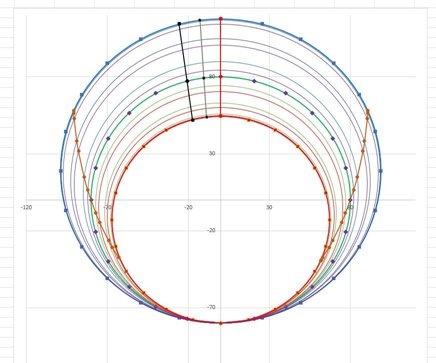
Figura 1: Gráfico obtenido en Excel para un reloj de sol elíptico reticular

Viendo el gran circulo que queda en el centro, se me ocurrió la idea de insertar un reloj de sol horizontal clásico de ángulo horario y diseñar un gnomon con dos estilos, uno para cada tipo. De esta forma se obtendría un doble horizontal que sería autorientable. Lo primero fue crear unas macros de Excel y de VBA para convertir los datos obtenidos en coordenadas X e Y para un programa CAD, tal como la versión gratuita de NanoCAD v.:5.0 [5] y dibujarlo.

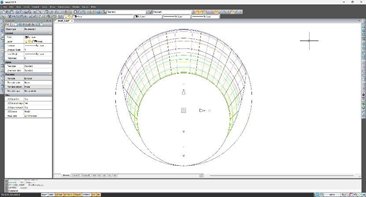
El reloj de sol horizontal de ángulo horario lo calculé con ayuda del programa Shadows Pro [6] y lo inserté en el dibujo CAD haciendo converger las líneas horarias de este en el punto en que convergen las del reloj de sol elíptico.

Trabajar con un programa CAD permite insertar, recortar y añadir líneas de forma más sencilla. De esta forma fue fácil dividir el reloj de sol horizontal para el espacio necesario para el gnomon.

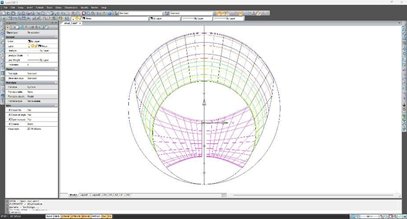
Figura 3: Elíptico y horizontal cásico en el programa CAD

Para dar distintos estilos y colores a las líneas, añadir textos y otros elementos y generar un fichero de gráficos vectoriales que facilitase el grabado, utilice Corel Draw.

En este paso añadí también un gráfico circular de la Ecuación del Tiempo, las coordenadas de mi emplazamiento (Logroño, España) y la corrección por longitud. Con esta información, y la fórmula también incluida, se puede calcular la hora oficial.

Con todos estos datos se obtuvo el diseño definitivo del plano del reloj de sol que puede verse en la Figura 4. En cada reloj de sol se han trazado las líneas de declinación correspondientes a al primer día de cada mes y las de los equinoccios y solsticios.

En el reloj de sol elíptico se han incluido las líneas de los ortos y de los ocasos que delimitan las zonas sombreadas a cada lado. Esto permite determinar de forma aproximada la duración del día para una fecha dada.

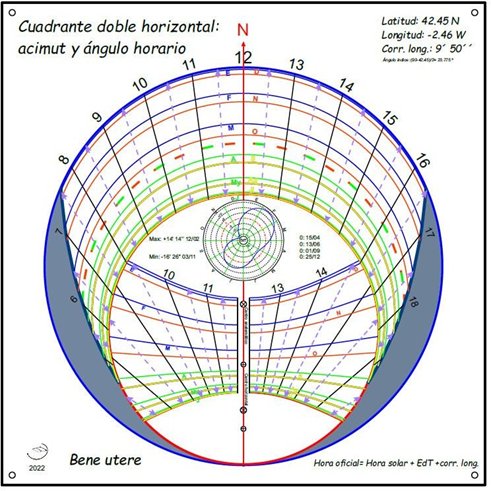
Figura 4: Elíptico y horizontal cásico en el programa CAD

Ahora había que diseñar un gnomon o elemento que proyecta la sombra, que permitiese leer el tiempo solar verdadero en ambos relojes de sol. Para ello debería tener:

Un estilo polar con una inclinación respecto al plano igual a la latitud del emplazamiento. El origen estaría en el punto donde convergen todas las líneas horarias y su longitud debería proyectar sombra durante todo el año en el reloj de sol horizontal. Debería incorporar un nodo que permitiese leer la fecha en las líneas de declinación.
Un estilo con una inclinación igual a (90 + Φ)/2 respecto al plano, donde Φ es la latitud. El origen estaría en el centro de la circunferencia de los equinoccios y tendría la longitud necesaria para proyectar sombra dentro de la línea correspondiente al solsticio de verano durante este.

Con esos parámetros y los requerimientos técnicos de espesores y taladros necesarios para su anclaje al plano del reloj de sol, diseñé el siguiente perfil en un programa CAD.

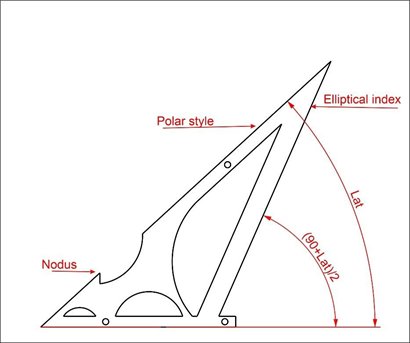
El fichero dxf sirvió para generar la figura en 3D por medio del programa FreeCAD [7].

La pieza tiene un espesor de 6 mm con el fin de permitir los agujeros para el anclaje el plano. Este espesor es el del estilo polar que ya se ha tenido en cuenta en el trazado del reloj de sol horizontal.

Sin embargo, el índice elíptico tiene que ser una arista afilada. Como pensaba construir la pieza con una impresora 3D, decidí diseñar la pieza en dos mitades en cuña y unirlas para obtener la arista.

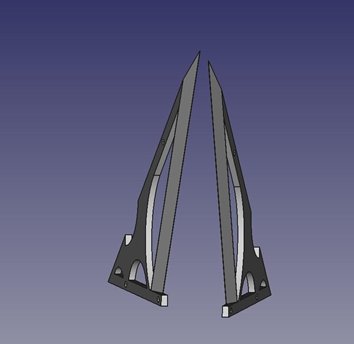
Figura 6: Diseño de las dos mitades del gnomon

Fabricación

La tabla del reloj de sol se grabó en una chapa de aluminio lacado en blanco de 1.5 mm de espesor por impresión UV, una técnica de impresión de precisión, en color y resistente, por una empresa especializada de Vitoria (España).

Las dos piezas para formar el gnomon se construyeron con una impresora 3D en mi casa.

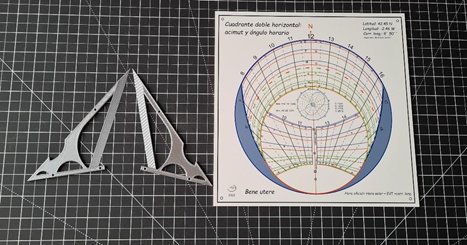
Figura 7: Elementos del reloj de sol antes del ensamblaje

Tras el ensamblaje de las dos mitades del gnomon y el montaje en el plano, se obtuvo el conjunto completo.

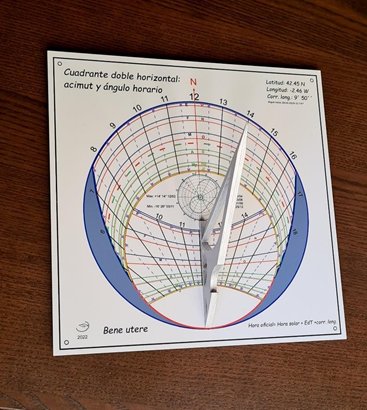
Pruebas

Con todo terminado, había llegado el momento de comprobar su funcionamiento. El 2 de octubre de 2022 coloqué el reloj de sol bajo el Sol. Como la fecha era fácil de identificar en ambos relojes de sol por su proximidad al comienzo de mes, fue muy sencillo hacer coincidir las horas y obtener una alineación perfecta.

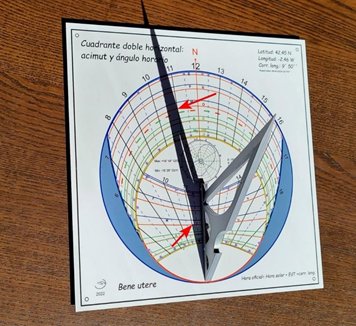
El funcionamiento desde el punto de vista gnomónico era perfecto, pero al pasar los minutos y acercarse el mediodía surgió un problema común en este tipo de relojes.

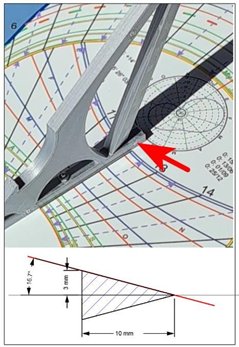
Como se ha dicho anteriormente, el índice del reloj de sol elíptico es la arista de una cuña y cuando el acimut del Sol se acerca a la línea meridiana, la arista entra dentro de la sombra de la cara posterior y es esta la que marca el acimut de forma errónea. En este caso el ángulo en que la lectura es errónea está comprendido entre +/- 16.7º y en la Figura 10 se puede ver el efecto y el motivo.

Buscando alternativas

La impresión 3D en casa proporciona la libertad de construir prototipos de forma fácil, rápida y económica. Solo debes tener una idea, dibujarla y en unas horas tocarla y probarla.

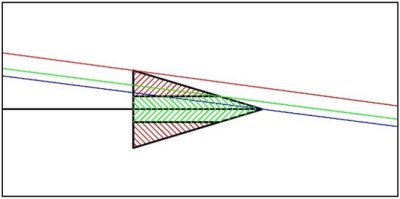
Una primera solución consistió en convertir la cuña en una lámina de 2 mm terminada en una arista. Como se ve en la Figura 11 esto permite reducir el error a una tercera parte del de la cuña en el ángulo en el que se está en la sombra de la cuña.

Figura 12: Reloj de sol con el índice en forma de lámina

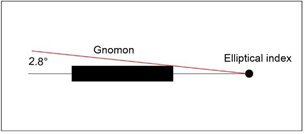
Otra solución consistió en modificar el gnomon para sustituir la cuña por una varilla de 3 mm de diámetro, que yo tenía en casa de otros trabajos, y que actuaría como índice del elíptico.

Ahora el índice del reloj de sol elíptico solo se ve afectado por la sombra del estilo del reloj de sol horizontal que en la situación más desfavorable se encuentra a una distancia de 30 mm con lo que el ángulo a partir del cual dejará de ser útil será 2.8º a cada lado de la meridiana. Esto también ocurre en el caso del índice en forma de cuña o de lámina.

Una vez impreso y ensamblada la varilla, el gnomon completo queda como se ve en la Figura 15.

Sustituyendo el gnomon de cuña por el de varilla, el reloj de sol se muestra en la Figura 15 y ya iluminado por el Sol en la Figura 16.

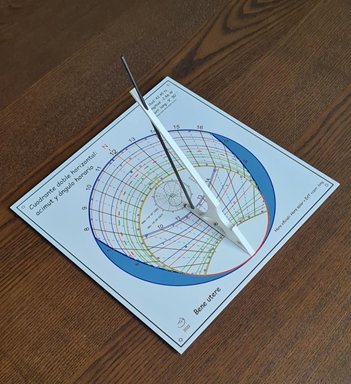
Si bien es cierto que con esta disposición se puede utilizar el reloj de sol elíptico en horas más próximas al mediodía, ahora la lectura de la hora en él es menos precisa ya que debe hacerse en el centro de la sombra de la varilla y no en el límite nítido de la sombra de la arista.

Figura 17: Reloj de sol doble horizontal con gnomon de varilla

Conclusión

Después de tantos meses de trabajo, el resultado obtenido superaba con creces las expectativas iniciales. Mi reloj de sol es original, completo y preciso.

Este trabajo me ha servido para maravillarme con las investigaciones y desarrollos teóricos realizados durante siglos por genios como Samuel Foster, Vaulezard, Wiilliam Oughtred y otros muchos y que, actualizadas y modernizadas por expertos contemporáneos como Fred Sawyer, Denis Savoie, etc, permiten a aficionados con trabajo, paciencia y utilizando modernas herramientas de cálculo y diseño realizar nuevos conceptos de relojes de sol.

Por otra parte, la utilización de herramientas como la impresión 3D facilita la experimentación y la fabricación de diseños más eficaces de forma económica y rápida, aunque nunca podrán llegar a ser las obras de arte creadas por los artesanos.

César Busto
Marzo de 2024

Este artículo ha sido traducido y publicado en el nº 30/2 de junio de 2023 de la revista The Compendium editada por la North American Sundial Society