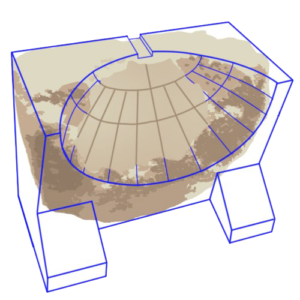
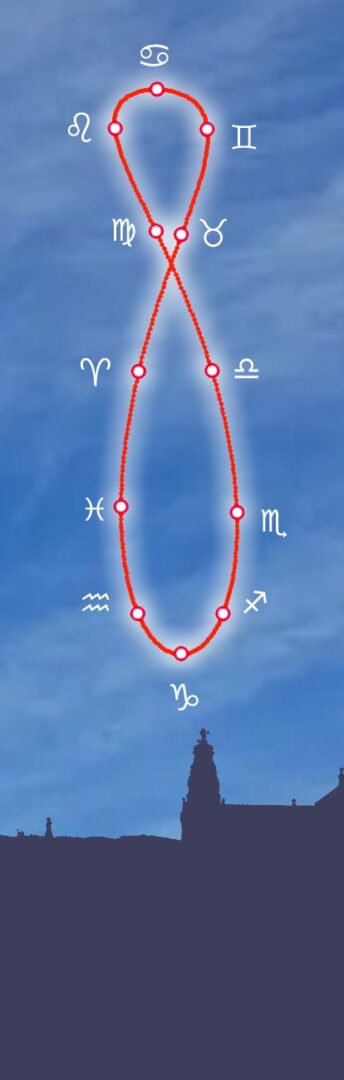
Analema solar sobre la ciudad de Córdoba

Existen relojes de sol en los que las líneas horarias rectas han sido sustituidas por unas líneas curvas en forma de «ocho» aunque lo más habitual, en el caso de encontrar dibujadas estas líneas curvas, es que sólo se tracen para la hora central del día y de esta forma no enmarañan la lectura: son las conocidas como meridianas o relojes meridianos.

Pero ¿cuál es el origen de ese trazado? ¿Por qué en lugar de una línea o acompañando a ésta, aparece trazada una curva o lemniscata?⁽¹⁾ En las líneas siguientes trataremos de explicar su origen, significado y su traslación a un plano vertical orientado a mediodía.

El analema solar del mediodía

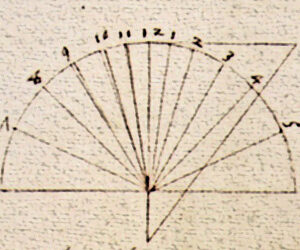
Para el cómputo horario la duración del día la hemos dividido en 24 horas iguales que tiene origen en la división en 24 tramos de 15 grados cada uno que aparentemente son recorridos por el Sol sobre el firmamento (cuando en realidad corresponde al movimiento de rotación terrestre).

Pero el giro de la Tierra alrededor del Sol sobre su eje inclinado ni es constante ni el eje se mantiene inclinado con la misma graduación. Las diferencias de la velocidad periférica respecto al ecuador celeste pueden llegar hasta el 13%, de ahí que los astrónomos establecieran junto al Sol real que mide el tiempo en tiempo verdadero (Tv) un segundo Sol ficticio que recorre el firmamento a la misma velocidad a lo largo de todos los días del año, aunque a diferente altura sobre el horizonte del lugar de observación. De esta forma es como se determina el Horario medio local o tiempo medio (Tm).

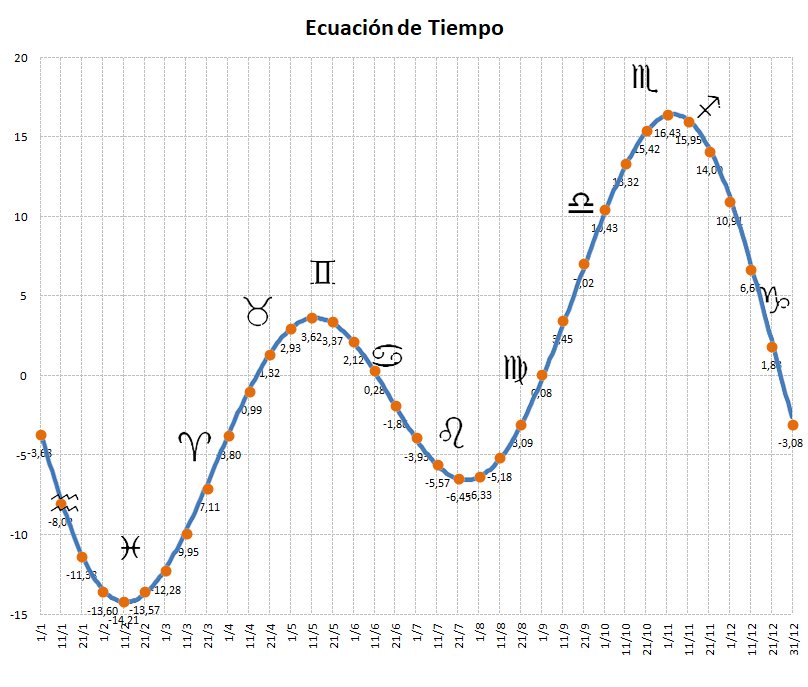
Y si a la inclinación del eje de rotación terrestre sobre el plano de la eclíptica, unos 23º27’ le añadimos que la Tierra no gira en círculo alrededor del sol sino que, debido a la excentricidad de su órbita, recorre una elipse y que, conforme a la segunda Ley de Kepler, dicho recorrido no lo hace siempre a la misma velocidad podremos observar que el Sol real a lo largo del año, a las doce del mediodía no siempre se sitúa en el Sur sobre una línea que denominamos meridiano del lugar sino que sufre ciertos atrasos o adelantos sobre esa línea gracias a la denominada Ecuación de Tiempo (EdT) que es la diferencia entre el tiempo medio y el tiempo verdadero (EdT= Tm – Tv).

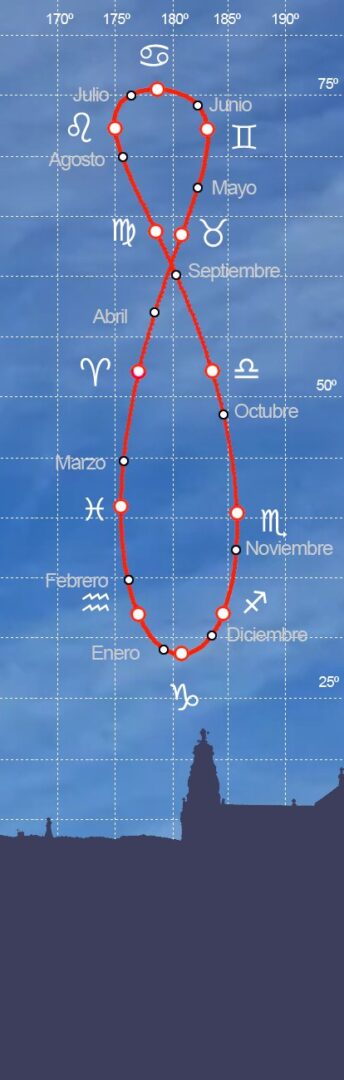
En base a esta premisa si nos situáramos frente a un mismo punto –por el ejemplo el Sur- y observáramos la posición del sol a la misma hora legal (con las salvedades de los adelantos del horario de verano o retrasos del horario de invierno) comprobaríamos que además de las distintas alturas en las que se posiciona el Sol a lo largo del año, no se sitúa sobre la línea vertical que parte del Sur geográfico, sino que por consecuencia de la EdT, durante unas épocas del año se sitúa al Este y otras al Oeste de esa línea meridiana formando su recorrido una curva en forma de «ocho»: es lo que conocemos como el analema solar.

Composición del analema solar

Teniendo en cuenta los datos de posición de una ciudad, que en nuestro caso hemos decidido que sea la de Córdoba y que hemos convenido se sitúa en el paralelo 37,88 grados norte, en el meridiano 4,78º oeste y a una altura de 138 m.s.n.m., hemos obtenido la posición del Sol sobre su horizonte para cada día del año⁽²⁾, situándolo en el firmamento gracias a una malla formada por los grados de acimut contados a partir del Norte y de la altura sobre el horizonte de la ciudad.

Cada uno de esos puntos de la superficie curva del cielo los trasladaremos a una superficie plana para lo que trazaremos una malla o sistema de coordenadas cartesianas (x, y), donde y=0º será el horizonte de la ciudad, ascendiendo poco a poco hasta el cénit del observador donde y=90º. En los gráficos que acompañamos no obstante, la altura sobre el horizonte la hemos limitado a 80º por no superar esa altura el Sol en ningún momento anual en su posición sobre la línea meridiana. En esa malla por tanto, los puntos “x” corresponden a los grados de acimut en sentido dextrógiro para un observador situado en el cénit, donde el grado 0 se situaría en el Norte, el Este iría situado en el grado 90 y el Sur, que es el que más nos interesa para la representación de la curva del analema solar sobre la meridiana, se sitúa en el grado 180.

No se trata pues ni de una proyección conforme, en la que se conservaría la relación angular entre distintos momentos de posición solar, ni equidistante ya que tampoco se conservan las distancias entre ellos, sino una simple proyección sobre un plano de los puntos en los que se sitúa el sol al mediodía para cada uno de los días del año. Ello hará que la curva que representamos se presente algo distorsionada sobre la curva real que se observaría sobre un firmamento que, a efectos de posicionamiento solar, suponemos esférico.

Sobre el eje cartesiano proyectaremos los puntos correspondientes a la posición del Sol al mediodía a lo largo de cada día, comenzando por el equinoccio de primavera en el que se sitúa en la eclíptica y, en todo caso en la colatitud cordobesa, a una altura de 52,12 grados sobre el horizonte de la ciudad, equivalente a la diferencia entre los 90º formados por el punto Sur sobre el horizonte y el cénit y la latitud geográfica que la hemos convenido situada en los 37,88 grados norte. En cuanto al acimut se localiza a 176,98º, es decir unos 3,02º antes del meridiano por lo que se dice que en ese momento el Sol atrasa, y que en este caso, conforme a la Ecuación de Tiempo alcanza los 7,41 minutos.

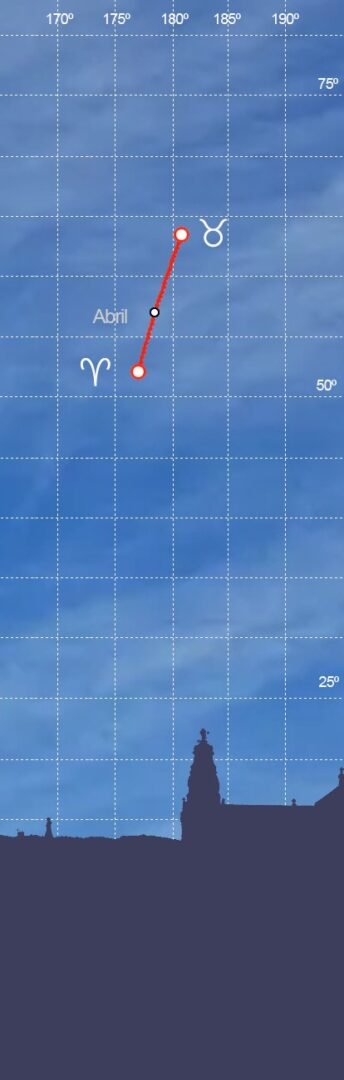
Pero a partir de esa fecha, el Sol poco a poco va ascendiendo –recordamos que la lectura siempre la haremos a la misma hora convencional- y atrasando cada vez menos hasta que el 15 de abril se sitúa sobre la meridiana y a una altura de 62,07º. Comprobamos que ése es uno de los cuatro días al año en los que el Sol ni atrasa ni adelanta con respecto al sol ficticio y de los que al final se mostrarán en tabla, junto a los que presentan mayores variaciones en más y en menos.

Tras esa fecha el sol adelanta llegando hasta los 3,7 minutos el 13 de mayo y sigue su ascenso en altura hasta el solsticio de verano en que alcanza su punto más álgido 75,55º pero presentando un retraso de 1,86 minutos sobre el sol ficticio. Unos días antes, el 12 de junio el Sol real volvía a coincidir con el sol ficticio sobre al meridiana.

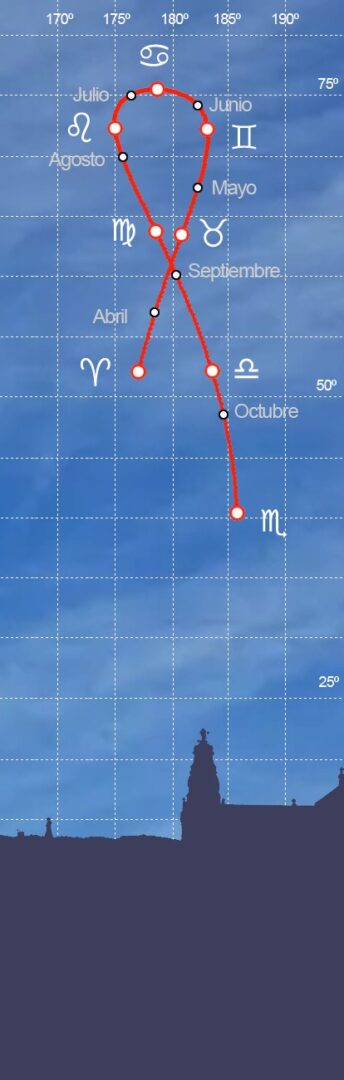
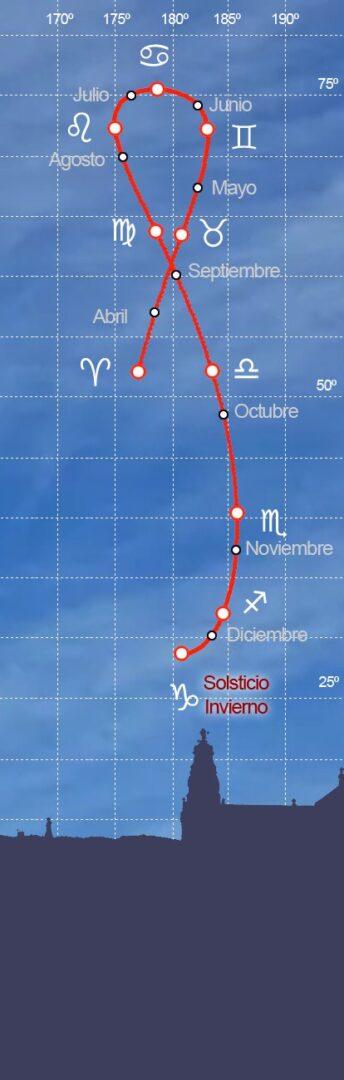
A partir de este solsticio el Sol comienza su descenso diario hasta que nuevamente el 1 de septiembre se sitúa sobre el sol medio y a partir de entonces nuevamente adelanta.

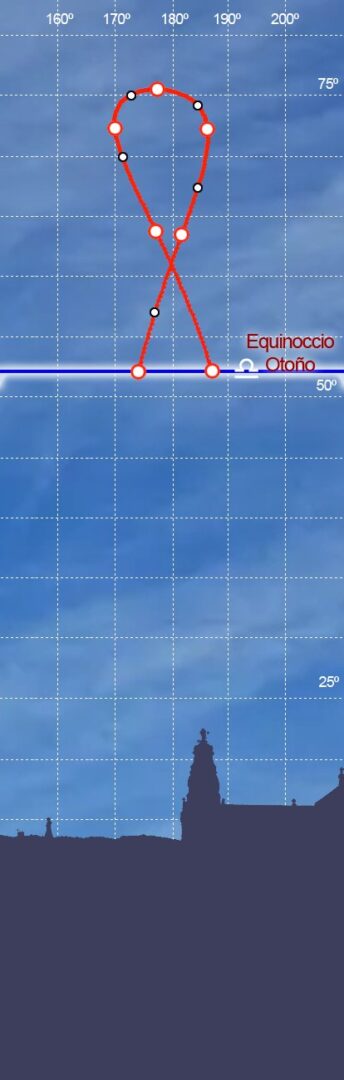
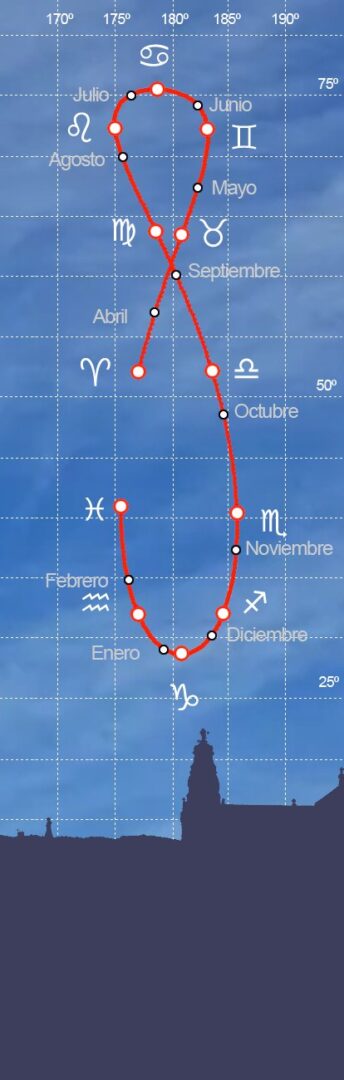
En el equinoccio de otoño, el 22 de septiembre, el Sol se sitúa en el punto de acimut 183,01º y a una altura de 52,19º sobre el horizonte continuando su descenso hasta alcanzar el solsticio de invierno, en su altura más baja sobre el horizonte, a tan solo 28,68º de altura y con un leve adelanto sobre el sol medio de 1,83 minutos. A partir de ese momento el Sol comienza a posicionarse a cada vez más altura sobre el horizonte –solo cuatro días después, el 25 de diciembre, nuevamente se observa la coincidencia del Sol real con el sol medio- y vuelve a atrasar, hasta que el 31 de diciembre alcanza los 3,10 minutos en espera de un nuevo año en el que nuevamente alcanzará el 11 de febrero con 14,20 minutos de atraso máximo de invierno.

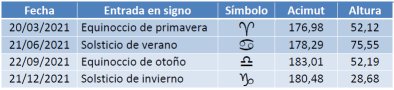
Para finalizar ofrecemos dos tablas en las que se reflejan algunos momentos anuales destacados. En la siguiente las fechas de entrada en cada estación, con indicación de grados de acimut y altura sobre el horizonte.

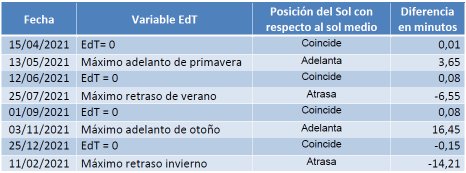
En la siguiente tabla se muestran los días en los que existe coincidencia entre el Sol real y el sol ficticio en el mediodía convencional y en los que producen las mayores diferencias entre ambos.

Otra cuestión es cómo trasladar el analema solar a las horas en un plano con el fin de que en él pueda ser leída la hora oficial -teniendo en cuenta además la corrección por la longitud, en su caso, y las adaptaciones horarias legales correspondientes- pero eso ya será objeto de otro estudio.

Esteban Martínez
Invierno de 2020/2021

Agradecimientos

• A Joan Serra Busquets, quien mediante su artículo Construcción teórica de un analema solar sobre una fotografía publicado en este mismo sitio, me ha hecho retomar el estudio sobre el analema solar.
• A Luis E. Vadillo Sacristán, de la Asociación de Amigos de los Relojes de sol, sin cuya inestimable ayuda no se podría haber realizado este estudio.

Notas

⁽¹⁾ En Gnomónica existe cierta discrepancia en la utilización del término analema que a veces es sustituido por lemniscata. En esta ocasión nosotros utilizaremos la definición analema exclusivamente para la curva solar y el término lemniscata a su proyección sobre un plano. Y esto por dos motivos: Porque en Matemáticas reciben este nombre las curvas en forma de ocho y para distinguirlo del término analemma (en griego αναλημμα) utilizado en geometría para la proyección ortogonal sobre un plano del camino del Sol en el plano meridiano a lo largo de las estaciones en un lugar determinado, tal como fuera descrito por Vitrubio en su obra “Re Architectura”. ▲

⁽²⁾ Los datos los hemos obtenido de la web Horizons, del California Institute of Technology. ▲