Corrección gráfica directa de la hora solar
Cuando nos planteamos realizar un reloj de sol, una de las dudas que surgen en primer lugar es sobre el tipo de lectura horaria que deseamos realizar en él ya sea en horario local real o tiempo verdadero, en horario medio local, para lo que hay que tener en cuenta la ecuación de tiempo, en horario de zona o convencional o, finalmente, que marque las horas teniendo en cuenta el ajuste horario con la adición de una hora para la de invierno y, en su caso, de dos horas para el caso en que se pretenda que el cuadrante lleve implícita la hora de adelanto estival.
Por todo ello, antes de proseguir definiremos un poco más ampliamente estos conceptos citados:
Convenciones horarias
- Horario local real o tiempo verdadero [tv]
Como los puntos determinantes para la luz y la oscuridad son la salida y la puesta del sol y éstos pueden variar hasta 4 horas, resulta más adecuado como punto de base para su medida los momentos del paso del Sol por los meridianos celestes de un punto de observación. La hora local es la misma en aquellos puntos situados sobre el mismo meridiano. Este es el horario que tradicionalmente han marcado los relojes de sol. - Horario medio local o tiempo medio [tm]
El giro de la tierra alrededor del Sol sobre su eje inclinado ni es constante ni el eje se mantiene inclinado con la misma graduación. Las diferencias de la velocidad periférica respecto al Ecuador pueden llegar hasta el 13%. Ante tales diferencias los astrónomos establecieron junto al ‘sol real’ un segundo ‘sol ficticio’ que se desplaza una vez al año en el fondo del firmamento y a lo largo del ecuador y con una velocidad constante y que era el que establecía la hora media local o tiempo medio. Para compensar estas diferencias horarias, en algunos relojes las rectas horarias son sustituidas por lemniscatas horarias o gráficos en forma que ocho, también conocidas como curvas del tiempo medio, en los que la compensación de tiempo horario no es necesaria aplicarla, puesto que mediante su lectura directa se corrige automáticamente la lectura del tiempo verdadero con respecto al tiempo medio de zona. El astrónomo francés Jean-Paul Grandjean de Fouchy fue el primero en utilizarlo en 1730 y en sus comienzos sólo se usaba para determinar con exactitud el mediodía de un lugar concreto.

Horario de zona o convencional
Cuando el sol se desplaza diariamente existen zonas que se encuentran más al Este o al Oeste que la nuestra. Pero ‘convencionalmente’ existen amplias zonas en que «es la misma hora»: Tienen el mismo horario de zona, término que sólo viene siendo utilizado tras la introducción de la convención del huso horario en la Conferencia Internacional de la Hora, celebrada en París en 1912.
Ajuste horario [ah]
Es la hora de adelanto decidida por los gobiernos, que hay que sumar a la leída en un reloj solar. En el caso del Estado español se viene aplicando desde la entrada en vigor del Real Decreto de fecha 26 de julio de 1900(1) mediante el que se dispuso la regulación de los servicios públicos de transportes y comunicaciones y de diversos organismos oficiales conforme al tiempo europeo occidental dando oficialmente por finalizada la utilización de los horarios locales habitualmente regidos por relojes solares en dicho tipo de horario. Tal medida fue adoptada de conformidad con diferentes propuestas -sobre meridiano universal, 24 husos horarios y conteo de las horas diarias desde 0 a 24- aprobadas en el Congreso Geográfico internacional de Washington, celebrado en 1888.
Adelanto de verano [av]
Adelanto de una hora que se viene realizando con el fin de que exista un mayor uso de la luz diurna y conseguir de esta forma un ahorro energético.
En la hemeroteca hemos encontrado esta primera noticia publicada en el nº 124 de la Revista Ibérica en 13/05/1916 en la que se da cuenta del debate mundial suscitado acerca del horario de verano y su implantación paulatina en distintos países.

Un mes más tarde se publicaba esta noticia en el nº 127 de la misma revista en la que ya se confirmaba la adopción del adelanto de verano por varios países europeos.

2ª edición del libro
Relojes de sol históricos. Tesoros andaluces olvidados

Finalmente la hora de verano fue implantada en España por primera vez en 16 de abril de 1918 tras la entrada en vigor del Real Decreto publicado en la Gaceta de Madrid del día 4 de abril, en el que se disponía la adopción de la hora de verano, por el que los relojes se debían adelantar 60 minutos a las 11 de la noche del 15 de abril, horario que debía durar hasta el 6 de octubre del mismo año.
Este adelanto horario actualmente se realiza en unos cincuenta países, incluyendo los de la Unión Europea en este caso en cumplimiento de una Directiva Comunitaria en vigor desde 1974.
Ecuación de tiempo [et]
La ecuación(2) de tiempo es la diferencia horaria que se da entre el movimiento aparente del sol verdadero y el sol medio, que es debida a la inclinación del eje de rotación terrestre sobre el plano de la eclíptica, unos 23º27’, y a que la Tierra no gira en círculo alrededor del sol, sino que, debido a la excentricidad de su órbita, recorre una elipse y, conforme a la segunda Ley de Kepler, a una velocidad que no siempre es la misma(3). En ocasiones la diferencia entre la hora solar real y la que se muestra en tu reloj de pulsera, alcanza hasta 16 minutos.
Por lo tanto:
et = tv – tm
En la tabla siguiente se ofrecen los valores medios para el año 2018 y en ella se observa que las diferencias más acusadas se producen los días 12 de febrero, 15 de mayo, 27 de julio y 4 de noviembre, sin embargo durante los días 15 de abril, 13 de junio, 1 de setiembre y 25 de diciembre no existe diferencia apreciable.

Adaptación horaria solar a la oficial mediante la Corrección Horaria
Dicho esto, y a pesar de que hemos realizado algunos relojes con horario adaptado a la longitud geográfica y a la hora legal, nuestro criterio actual, que es ampliamente compartido por la comunidad de gnomonistas y cuadranteros, es realizar relojes solares en tiempo verdadero y que nos indique la hora solar. En estos casos generalmente existirá una diferencia, en ocasiones sustancial, entre la hora leída y la hora oficial por lo que si queremos conocerla –siempre aproximada- deberemos aplicar la siguiente fórmula para lo que tendremos en cuenta las magnitudes que asimismo se señalan:
ho = hs + ah + av + cl + et
Donde:
| ho | Es la hora oficial, la que marca tu reloj de pulsera, tu celular, |
| hs | Es la hora solar, la que es leída en un reloj de sol con horario local real. |
| ah | Es el ajuste horario que es determinado por cada Estado según el huso de referencia. En el caso del español, excepto Islas Canarias, es de una hora de adelanto |
| av | Es el adelanto de verano, en nuestro caso de una hora, añadida en su caso al adelanto horario, durante el periodo que transcurre entre el último domingo de marzo finalizando durante el último domingo de octubre. |
| cl | Corrección por longitud geográfica. Para una mejor distribución horaria, desde la Conferencia de París, la esfera terrestre se ha dividido convencionalmente en 24 husos horarios, uno para cada hora y que son los que, fundamentalmente determinan la adecuación de una zona o un país a un horario legal de uso. Pero ocurre que en la mayoría de los casos el reloj de sol no se encuentra situado sobre el meridiano de referencia, sino que se encuentra unos grados al Este o al Oeste de él. Eso contribuye a que, en el caso de que esté al Oeste, el sol atraviese éste unos minutos antes que el correspondiente al lugar de lectura, por eso habrá que sumar unos 4 minutos a la hora solar leída por cada grado de diferencia, si nos encontramos al Oeste del meridiano de referencia o restarlos en misma proporción, si nos encontramos al Este. |
| et | Corrección debida a la ecuación de tiempo para lo que se tienen en cuenta los datos de la tabla citada más arriba pero en signo contrario. |
Así por ejemplo para «poner en hora» [ho] tu reloj de sol con horario local real [hs], en Córdoba, que se encuentra en el meridiano 4º 45′ al oeste de Greenwich, el día 12 de agosto, a las 12:00, deberás hacer la siguientes operaciones:
- Sumarle a la leída, la hora de ajuste horario [ah] con respecto al horario del huso que corresponde
- Sumarle la hora de adelanto estival [ae]
- Sumarle 19 minutos, 4 minutos por cada grado de Longitud geográfica [cl] ya que 4 * 4º 45’ (4,75) = 19 min.
- Sumarle 5,08 minutos de la ecuación de tiempo [et] que son los correspondientes a la fecha elegida en la que el sol real lleva ese atraso con respecto al sol ficticio que se tiene en cuenta para el cálculo en la hora oficial.
Por lo tanto la hora oficial vendrá determinada por la siguiente suma:

Nótese que aunque en la tabla para el día señalado la cifra incluida en la ecuación de tiempo es negativa nosotros la hemos incluido en la fórmula en positivo. Esto es así para compensar precisamente el tiempo de adelanto solar con respecto al sol medio.
Esta fórmula numérica de corrección horaria es la elegida por determinados autores como el Ing.º Juan José Muñoz Pérez quien a su numerosa obra desperdigada fundamentalmente por la costa gaditana, suele añadírsela aunque simplificada ya que bajo el título “Corrección Horaria” determina que la
HORA RELOJ = hora solar + adelanto + diferencia
especificando que adelanto es de 1 hora en invierno y de 2 en verano y que el valor de la diferencia, en minutos, incluye la corrección por longitud, es decir que ha optado por agrupar las magnitudes [ah] y [ae] en “adelanto” y [cl] y [et] en “diferencia”.
En estas instrucciones para la lectura no se señalan los minutos de compensación por la [et] para todo el año sino solo para los días 21 de cada mes, fechas cercanas a los momentos de entrada en cada uno de los signos zodiacales. Estos casos los podemos encontrar en los relojes de la Playa del Camaleón de Chipiona y del Paseo Marítimo de la Línea de la Concepción, como a continuación se muestra.
Curva de la ecuación de tiempo y su transformación en la curva de compensación de tiempo horario
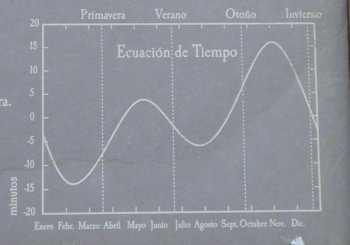
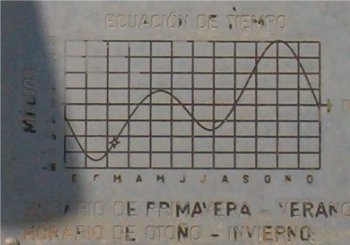
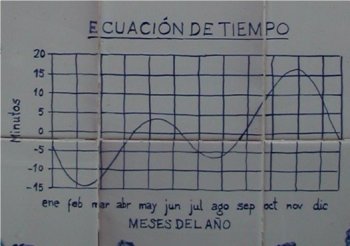
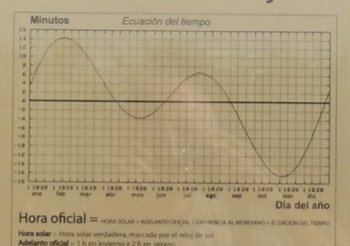
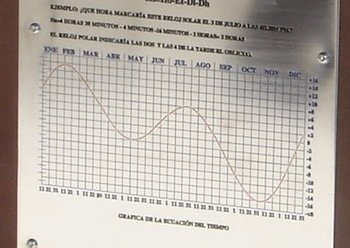
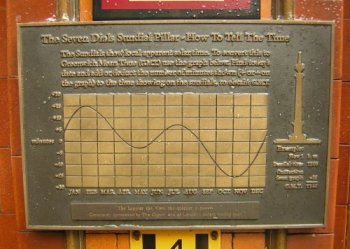
La ecuación de tiempo descrita dentro del primer epígrafe “Convenciones horarias”, también suele representarse mediante distintos tipos de gráficos aunque el más común es el modelo que a continuación se muestra en el que en un eje de coordenadas se reflejan los minutos aproximados de adelanto o retraso del Sol con respecto al sol ficticio para los distintos meses del año.

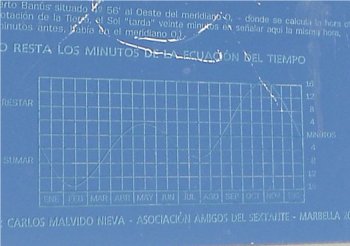
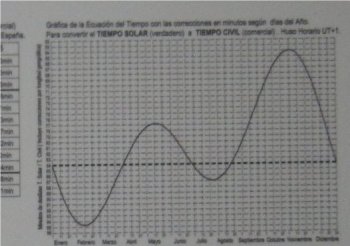
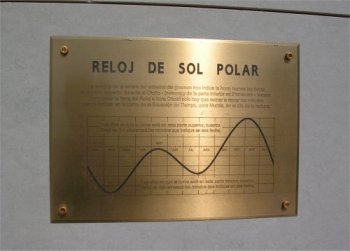
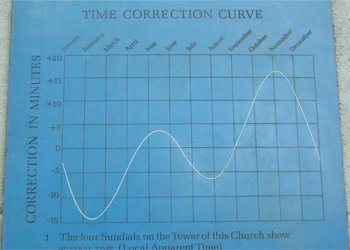
Este modelo de gráfico es ampliamente utilizado y suele colocarse en las cercanías de los relojes de sol junto con las instrucciones para la adaptación horaria eso sí especificando que cuando el sol adelanta unos minutos, esos mismos minutos se deben restar de la hora leída y al contrario. A continuación se muestran algunos ejemplos que acompañan a relojes solares diseminados por toda Andalucía y también de otras latitudes.

Pero ésta no es la única forma de representar gráficamente la ecuación de tiempo. También la curva de la ecuación de tiempo dispuesta verticalmente y con forma de lemniscata en la que en el eje de abscisas ahora se sitúa los minutos de adelanto o retraso horario conforme a la ecuación de tiempo y en el de ordenadas los grados de declinación solar con respecto a la eclíptica.
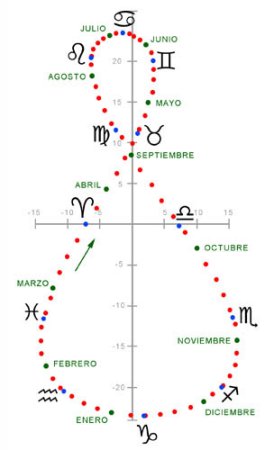
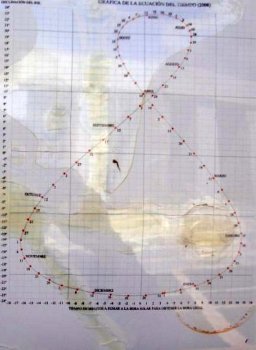
Así la encontramos dispuesta verticalmente en el reloj de sol de la Hacienda Merrha, de El Viso del Alcor o con forma de lemniscata, como el que estuvo situado, hoy desaparecido, al pie del dispositivo señalador del cuadrante horizontal monumental del Parque Los Olivares en Atarfe. En este último, además de señalarle los minutos de adelanto o atraso solar sobre el sol medio, se ofrecían los grados de declinación solar.

Pero si el sol se encuentra adelantado con respecto a ese sol ficticio para adaptar la hora conforme a este parámetro deberemos restar esos mismos minutos de adelanto a la hora leída. Y al contrario si el Sol atrasa deberemos sumar esos mismos minutos a la hora ofrecida por la sombra del reloj solar. En definitiva que para pasar de la hora solar en tiempo verdadero al horario medio local, se aplica la ecuación de tiempo pero cambiándole el signo. Eso significa que la curva de la ecuación de tiempo se invierte y se transforma en la curva de compensación de tiempo horario donde no se señala el retraso o adelanto solar sino directamente los minutos a sumar o restar a la hora leída.
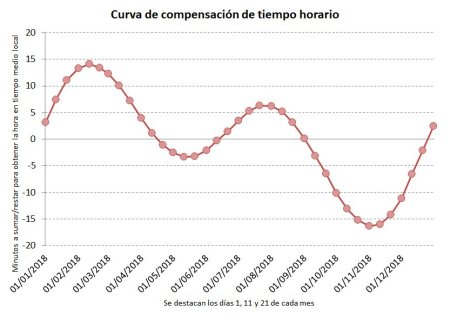
Esta curva de compensación de tiempo horario figura asimismo representada acompañando a relojes solares para su mejor lectura horaria. A continuación se muestran algunos ejemplos.
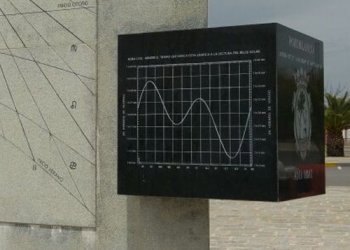
Al igual que ocurría con la curva de la ecuación de tiempo, también la curva de compensación de tiempo horario se puede representar en forma de lemniscata. En el ejemplo siguiente se muestra la existente en el Observatorio de la Marina de San Fernando, en el que se han destacado 16 días del año, sin que hayamos sabido encontrarle el motivo de su elección.

Adaptación de la curva de compensación de tiempo horario a la Longitud geográfica
Como hemos visto hasta ahora, lo habitual es representar las magnitudes para la corrección horaria individualmente o agrupándolas y sirviéndose para la corrección de la ecuación de tiempo de la ayuda de la curva de la ecuación de tiempo o de la curva de la compensación de tiempo horario, siempre referidos a los minutos de adelanto o atraso solar con respecto al sol medio.
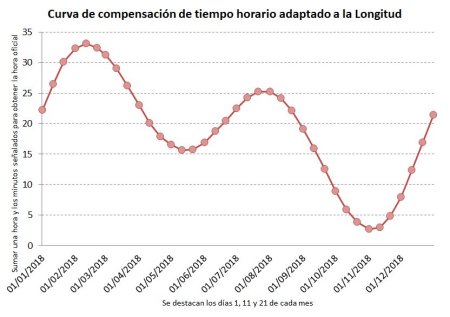
Pero, para obtener la hora oficial –insistimos, siempre aproximada- mediante la lectura de un reloj solar con horario local real o tiempo verdadero podemos acudir a una curva de compensación de tiempo horario que lleve implícitos los minutos para la corrección de lectura debidos a la ecuación de tiempo y que además incluya la corrección por longitud geográfica. En este caso a los minutos correspondientes al día elegido, sólo habría que sumarle la hora u horas de ajuste horario y adelanto estival. Nosotros pensamos que mediante este sencillo método se facilita la adaptación horaria.
A continuación se muestra un ejemplo, en este caso de curva de compensación de tiempo horario para 2018 adaptada a la longitud 4º 49’ oeste lo que implica un incremento implícito de 19,27 minutos sobre el horario del meridiano de Greenwich.
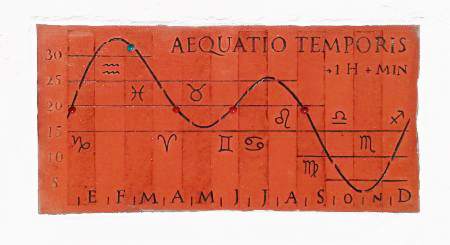
En la imagen siguiente se muestra la misma curva pero materializada sobre placa de barro cocido, mismo material que en el que se ha confeccionado el reloj de sol al que acompaña. En ella se han destacado mediante franjas verticales los periodos correspondientes a los signos zodiacales y la indicación de que para obtener el ajuste horario habrá que añadir a la hora de adelanto los minutos correspondientes para cada día de lectura. Asimismo se han señalado en rojo los cuatro días anuales en los que no se aprecia diferencia entre la lectura entre el sol real y el sol medio, y específicamente uno más, en color verde, para el día 28 de febrero, Día de Andalucía, fecha que asimismo se ha señalado en el correspondiente reloj-calendario.
Pensamos que con la expresión gráfica de la compensación de tiempo horario mediante una curva que lleve implícita la corrección por longitud y la indicación de la necesaria adenda de una o dos horas según la época, se facilita la conversión a la hora oficial de la hora obtenida de un reloj solar en tiempo verdadero ¡siempre con el permiso de las nubes!
Esteban Martínez
Enero de 2019
Notas
(1) Aunque probablemente sea mucho mayor el número de este tipo de cuadrante conservados y no sólo en esta Comunidad Autónoma ▲
(2) Trad. Latín: “La sombra enseña” ▲
(3) Las dimensiones que se mencionan se realizan estimativamente casi en todos los casos. ▲
Más noticias
- Revista Orologi Solari
- Un sombrero para el sol
- Visita guiada al Museu del Rellotge
- Proyecto de ruta solar cultural en Zaragoza
- El arte de hacer relojes de sol
- Calendario gnomónico – Enero 2026
- Una bola para el árbol de Navidad
- Nueva conferencia on line prevista con motivo del WSD 2026
- Nuevo espacio para Claude Gahon en nuestra sección de Autores
- El compendio gnomónico de Ulrich Schniep
- Revista «Analema»
- Disponible en pdf el libro de los relojes de sol de A Coruña