Construcción teórica de un analema solar sobre una fotografía
Llamamos analema solar o lemniscata a la figura en forma de “8” que recorre el sol durante un año si observamos su posición a la misma hora oficial cada día y en el mismo lugar. Hay que señalar que la palabra analema no figura en el diccionario de la RAE, en cambio sí lo hace la palabra lemniscata que significa lo mismo pero que, sin embargo, en el ámbito de la astronomía y de la gnomónica, se usa más la palabra analema. Esta figura es la representación “en vivo” de la Ecuación del Tiempo, es decir, la diferencia que hay entre la hora solar o de tiempo verdadero y la hora que marcan nuestros relojes de pulsera.
Como se ha dicho, un analema es la representación del recorrido del sol durante un año a la misma hora oficial cada día y una forma de constatarlo es colocando una cámara fotográfica en un lugar fijo por donde pase el sol a una hora determinada e ir tomando fotos a esa misma hora cada día del año o en intervalos semanales o quincenales, a elección de cada uno. Al cabo de un año obtendrá una imagen como la siguiente.
Si en lugar de fotografiar el sol a la hora oficial se hiciera a la hora solar o de tiempo verdadero, la imagen sería una recta.
Viendo estas fotografías siempre he pensado que la construcción de un Analema mediante fotografías periódicas a la misma hora durante un año era una labor no apta para impacientes crónicos, tal como yo, pongo por ejemplo. Una labor, por otra parte, digna de mi admiración por la técnica, constancia y perseverancia que implica el hecho de fotografiar el sol con la misma posición de la cámara enfocada al mismo lugar cada equis días a una hora determinada, siempre la misma teniendo en cuenta los dos cambios de horario, y que incluye un buen número de frustraciones debido a nubes, lluvias, y otros impedimentos, meteorológicos o no. Siempre he admirado, digo, que a pesar de todo se consigan estos resultados espectaculares como podemos apreciar en la foto de la catedral de Palma tomada el día del solsticio de invierno cuando la luz del sol naciente entra por el gran rosetón del Este y, atravesando la nave central, sale por el rosetón del oeste originando un efecto espectacular.
Pero yo, que no poseo ninguna de esas virtudes y sin embargo sentía el gusanillo de construir un analema decidí intentar abreviar el procedimiento.
He de confesar que me siento satisfecho del resultado si bien los más puristas dirán, no sin razón, que he sacrificado la exactitud, y lo reconozco. Sí, porque con mi método, basado en el cálculo teórico sobre una fotografía base, se producen por fuerza varios errores pero que, en mi opinión no desmerecen ni el esfuerzo ni el resultado. Errores propios de una fotografía, como la distorsión o aberración en los extremos laterales en función del objetivo, error en la exactitud del azimut y altura de los puntos tomados como referencia y, en fin, errores al trasladar las coordenadas del sol en cada fecha sobre la fotografía base, sin olvidar el error implícito per se al intentar plasmar sobre un plano bidimensional posiciones tridimensionales de una esfera.
Aun así lo he construido e intentaré explicar cómo lo he compuesto por si a alguien le puede servir y sobre todo mejorar el método reduciendo los errores.
Justo enfrente del balcón de mi casa (en Palma de Mallorca) tengo el campanario de la iglesia de Ntra. Sra. Del Socorro, o como también la llaman, la iglesia de santa Rita que forma parte del colegio de San Agustín que se ve en primer plano.
El campanario, de planta octogonal con caras notoriamente desiguales, consta de nueve cuerpos o pisos de altura, sin embargo, solo los tres últimos, que son los que veo desde casa, poseen las ventanas que se observan. En total, hasta la cúspide del chapitel mide 47 m de altura. Como curiosidad añadiré que en dos de sus caras, las que miran al sur y al suroeste poseen sendos relojes de sol en buen estado aunque con los gnómones fuera de servicio. El que suscribe, se ofreció a la propiedad para gestionar la restauración de los gnómones y dejar de nuevo los relojes operativos. La idea fue gratamente acogida bajo la ilusoria suposición de que a la propiedad le saldría gratis toda la intervención, incluida la colocación del andamiaje necesario. Ante esta irrevocable suposición, el que suscribe se acordó de una célebre frase de El Quijote. Allí siguen los relojes.
En febrero y en octubre, durante unos días sucesivos, el sol en su camino hacia la puesta pasa por cada una de las tres ventanas del campanario como puede apreciarse en la siguiente foto.
Escogí una imagen de las múltiples tomadas en la que el sol pasa por la ventana central y que muestra un horizonte bastante amplio.
A partir de esta imagen en la que tenía el sol perfectamente situado en acimut, altura, día y hora, tracé un emparrillado teórico de acimuts y alturas. Para los acimuts fue más sencillo ya que podía determinar con exactitud cada uno de los puntos de los edificios que tomaba como referencia y, para las alturas, conocidas las de cada ventana y la del extremo o vértice del campanario completé la parrilla siendo consciente de que las coordenadas de alturas no eran del todo precisas pero que, debido al tamaño de la foto la poca diferencia que pudiera haber no alteraría demasiado el resultado.
Mediante uno de los múltiples programas y aplicaciones de fácil acceso en los que se puede conocer la posición solar para cualquier momento del año fui tomando nota del acimut y altura del sol cada siete días a la misma hora de tiempo oficial. Una sencilla hoja de cálculo me convertía estos datos en distancias horizontales y verticales a partir de un punto elegido como origen de coordenadas. Particularmente en este caso elegí el sol en la ventana como origen pero hubiese podido ser cualquier otro como un extremo cualquiera, por ejemplo. En cada una de estas coordenadas fui colocando cada uno de los soles hasta completar la figura. Una vez finalizada tuve que eliminar algunos soles, especialmente en la curva perteneciente al verano porque se solapaban y alteraban demasiado la estética de la figura, quedando, al final, el resultado que se ve en la siguiente foto.
Satisfecho y animado por el resultado y aprovechando la hoja de cálculo, tomé la posición solar de los mismos días pero correspondiente a cada una de las dos horas anteriores y de la posterior y de la misma forma construí los otros tres analemas.
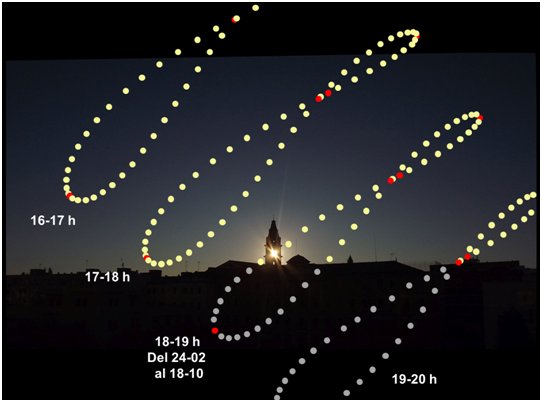
Los días en que la Ecuación del Tiempo es cero los he señalado en rojo y me he permitido prolongar los analemas que quedarían debajo del horizonte para que se vea su inclinación.
El eje del analema es la línea que pasa por los puntos de ecuación cero y que por norma general suele ser una recta. En la fotografía siguiente puede observarse que el eje de los analemas no es una recta sino una ligera curva o arco debido a la distorsión o curvatura que presenta el analema. La causa de esta distorsión la encontramos en el hecho de que los resultados de los cálculos plasman una imagen de la esfera celeste, esférica, es decir, un arco de meridiano, al trasladarlo sobre un plano bidimensional aunque, en la realidad, en el cielo, no se vería esta distorsión, pero sí que se observa incluso en las fotografías de analemas realizadas mediante cámaras estenopeicas que carecen de lente.
Este eje, que representa un meridiano de la esfera celeste, se curva de tal manera que solo es paralelo al eje Norte – Sur en el punto de intersección del meridiano con el ecuador celeste. Por otra parte, sabemos que el ángulo entre el horizonte y el eje Norte-Sur es igual a la latitud del lugar. Los dos únicos meridianos cuyo punto de intersección coincide con el ecuador celeste y el horizonte son los meridianos de las 6h y 18h. Por tanto, la inclinación de sus ejes con el horizonte será igual a la latitud.
Para ratificar que el método es aceptable he construido el analema de las 19-20h que corresponde al meridiano de las 18h UTC y cuyo ángulo de inclinación coincide con la latitud de Palma de Mallorca. Para ello, he tenido que construirlo entero, o por lo menos los puntos de ecuación cero para poder trazar el eje. Sin embargo, cuando no sea posible, se puede tomar la inclinación del analema completo más cercano a esta hora que, si bien no dará el ángulo exacto, sí que nos dará un valor aproximado.
Como conclusión, y consciente que soy de que será rechazado, con razón, por la rama más purista de la comunidad gnomónica reitero una vez más que el método aplicado es heterodoxo, que acumula una serie de pequeños errores pero perfectamente válido como ejercicio para hacerse una idea de cómo quedaría el analema fotografiado día a día. Debo decir que si bien ha sido un ejercicio laborioso también ha sido entretenido y gratificante que me ha ayudado a soportar mejor el confinamiento obligatorio debido a la actual pandemia.
Joan Serra Busquets
Otoño de 2020
(1) Como el desafortunado encalado de su fachada que lucía en 1931, tal como puede verse en el blog http://baruntoboronia.blogspot.com/2018/08/cuando-confundo-la-vaquera-con-el-reloj.html. ▲
(2) RUIZ H. Libro de arquitectura ms, 1566; fo 32 V.»Reloj para pared que no está derechamente al medio día», según se señala en ESTEVE C La ciencia gnomónica en la España del siglo XVI: Análisis, desarrollo y evolución de las técnicas horolográficas. Universidad de Granada. Granada 2003. ▲
(3) PUERTO FERNANDEZ M.I. Ecclesia Igneus. Reconstrucción del patrimonio perdido. TFM. Univ.Granada. Granada, 2016, pág. 30. ▲
(4) Como asimismo se menciona en ESTEVE C. La Ciencia gnomónica. ▲
(5) PEREZ DE MOYA, J. Fragmentos mathematicos en que se tratan cosas de Geometría y Astronomía y Geographia y Philosophia natural. Esfera y Astrolabio y Navegación y relojes. Salamanca, 1568. ▲
(6) ROIZ, P. Libro de reloges solares. Casa de Pedro Huete. Valencia, 1575. ▲
(7) ARFE Y VILLAFAÑE, J. De varia commensuracion para la esculptura y architectura. Sevilla, 1585. ▲
(8) En los relojes de sol se denominan veneras a las líneas horarias por similitud con los pliegues radiales que presentan las conchas de las vieiras. ▲
(9) La cifra 2 como “Z” se encuentra asociada a la cifra 5 como falciforme invertida en los relojes de sol fechados del primer tercio del siglo XVII. Ver NOVELLA P. Relojes de sol. Generalidades. (976-1900). Edición del Autor, 2020. ▲
(10) Como se señala en NOVELLA P. Relojes de sol de meridiana esviada. Edición del autor. 2020, “Relojes de meridiana desviada son los relojes de sol situados en paredes declinantes que no tienen la línea de las doce en posición vertical. Se les ha dado ese nombre porque de alguna manera debían nombrarse para distinguirlos en las clasificaciones. Son relojes que no marcan bien las horas. No entran en este grupo de clasificación, los relojes de sol bien calculados con la longitud corregida.” ▲
(11) LLERA FUEYO F.J. Relojes de sol en el Principado de Asturias, I. Edición del Autor. 2012. Pág. 22. ▲
(12) Entendiendo como tal todo reloj solar que ha sido realizado con anterioridad al siglo XX o, en todo caso, si tienen más de 100 años de antigüedad. ▲
(13) Ver www.boe.es/boe/dias/1981/03/18/pdfs/A06001-06001.pdf. La Ley 16/1985, de 25 de junio, del Patrimonio Histórico Español, protege como BIC los bienes inmuebles integrados en el Patrimonio Histórico Español, como son los monumentos históricos, incluyendo “Todo lo que esté unido a un inmueble de una manera fija, de suerte que no pueda separarse de él sin quebrantamiento de la materia o deterioro del objeto”, como es el caso del reloj solar de la Catedral de la Sierra. ▲
(14) Por desgracia no corrió la misma suerte la cercana iglesia de San Andrés de Alcaracejos, muy probablemente construida por los mismos canteros que la Catedral de la Sierra, destruida por las bombas tras el infame levantamiento militar en 1936 contra el régimen democrático y republicano establecido. ▲